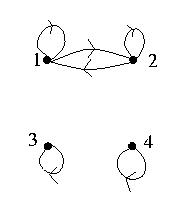
3. R2 = { (1,1), (1,2), (2,1), (2,2), (3,3), (4,4) } is an equivalence relation. The elements 1 and 2 are related to each other in every way, but the elements 3 and 4 are both isolated (they occur in the graph as single vertices with loops on them).

Thus the partition of the set {1, 2, 3, 4} is {1, 2} {3} {4}.
There are three equivalence classes of R2 : [1] = [2] = {1, 2}, [3] = {3} and [4] = {4}.
R6 = { (1,1), (2,2), (3,3), (4,4) } is an equivalence relation. However all four elements are related only to themselves (they occur in the graph as single vertices with loops on them).

Thus the partition of the set {1, 2, 3, 4} is {1} {2} {3} {4}.
There are four equivalence classes of R6 : [1] = {1}, [2] = {2}, [3] = {3}, [4] = {4}.