Solution for Section 3.5 Question 5
5. Suppose that n is an odd integer. We need to show
that 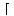 n / 2
n / 2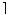 =
= 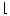 n / 2
n / 2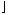 + 1.
+ 1.
Proof Since n is an odd integer, n = 2k + 1
for some integer k.
| Left-hand side: |
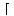 n / 2 n / 2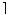 = = 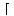 (2k
+ 1) / 2 (2k
+ 1) / 2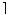 = = 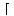 k + 1/2 k + 1/2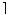 = k + 1 (by the definition of
ceiling, see illustration below). = k + 1 (by the definition of
ceiling, see illustration below). |
| Right-hand side: |
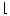 n / 2 n / 2 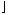 + 1 = + 1 = 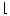 (2k + 1) / 2 (2k + 1) / 2 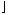 + 1 = + 1 = 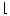 k + 1/2 k + 1/2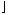 + 1 = k + 1 (by the definition of floor, see
illustration below). + 1 = k + 1 (by the definition of floor, see
illustration below). |

Thus 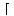 n
/ 2
n
/ 2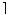 =
= 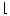 n / 2
n / 2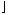 + 1.
+ 1.
Back to Section 3.5
![]() n / 2
n / 2![]() =
= ![]() n / 2
n / 2![]() + 1.
+ 1. 
![]() n
/ 2
n
/ 2![]() =
= ![]() n / 2
n / 2![]() + 1.
+ 1.