Hint for Section 4.2 Question 2b

2b)

Let P(n) be the claim: n

     1    

j (j + 1)

=

    n   

n + 1
for all integers n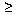geq.jpg (602 bytes)1.
S
j = 1
P(1) is the statement: 1

     1      

j (j + 1)

=

   1  

1 + 1
S
j = 1
P(k) is the statement: k

     1     

j (j + 1)

=

    k    

k + 1
S
i = 1
P(k+1) is the statement: k + 1

     1     

j (j + 1)

=

  k + 1 

k + 2
S
i = 1

For a proof by induction, you first need to check that the statement P(1) is true. Then assume that P(k) is true and use this to show that P(k + 1) is true.

 

The statement P(1) is true since 1

     1    

1 (1 + 1)

=

   1  

=

1

1 · 2

2
S
i = 1

Now assume that the statement P(k) is true. We now need to show that the left-hand side of P(k+1) is equal to the right-hand side of P(k+1).

L.H.S of P(k+1)

=

 k + 1

     1    

j (j + 1)
S
i = 1

=

 k

     1    

j (j + 1)

+

          1          

(k + 1) (k + 2)
S
i = 1

Use your assumption that the statement P(k) is true to simplify this expression. Your goal is to end up with the right-hand side of P(k+1).

Back to Section 4.2
Full solution