1a) Let w represent "wages are raised", let b represent "buying increases", and let d represent "there is a depression." Now write each of the premises and the conclusion in symbolic form.
The first premise (p1) is "If wages are raised, then
buying increases." This can be written symbolically as w
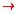b.
The second premise (p2) is "If there is a depression, then wages are not
raised." This can be written symbolically as d 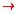~w.
The conclusion (q) is "Therefore, either there is not a depression, or wages are not
raised." This can be written symbolically as ~d
V ~w.
Remember that an argument is written as a conjunction of the premises
implies the conclusion. So this argument can be represented as
[(w 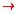b) L (d 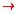~w)]
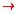(~d V ~w).
To determine if it is possible for an argument to be invalid, we are looking for truth values for the variables which make the conclusion false but all of the premises true.
Fill in the following steps:
For the conclusion ~d V ~w to be FALSE, we need d to be TRUE and w to be TRUE.
For the premises to be TRUE we need w
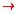b to be true (1) and d 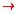~w to be true (2).
Can you find a set of truth values for w, b and d, which make the conclusion false but the premises true?
For the premise w 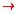b to be true we need either: w to be TRUE and b to be TRUE, or w to be FALSE.
So far the first premise can be true while the conclusion is false by letting d, w and b all be true.
For the premise d 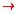~w to be true we need either: d to be TRUE and w to be FALSE, or d to be FALSE.
Is is possible for the first and second premises to be true while the conclusion is false?
NO. There is no set of truth values which make both premises true and the conlusion false. Hence there is no combination of truth values which makes this argument invalid so the argument must be valid.