Chapter One
The Logic of Compound Statements
Section 1.1
Logical Form and Logical Equivalence
The following solutions use information found on pages 1-14 of the textbook.
Exercise 1.1.1: Definitions
Fill in the blanks to complete the following sentences.
- A statement or proposition is a
sentence that is true or false but not both.
- If p is a statement variable, the negation of p
is "not p" and is denoted ~p.
It has the opposite truth value from p: if p
is true, then ~p is false; if p is
false, then ~p is true.
- If p and q are statement variables, the conjunction
of p and q is p L q,
which is read "p and q". p L q
is true when both p and q are true. p
L q is false when at least one
of p or q is false.
- If p and q are statement variables, the disjunction
of p and q is p V q, which is read "p or q". p V q is true when at least one of p or q is true. p
V q is false when both p and q are false.
- A statement form or propositional form is an expression made up of statement variables (such as p, q
and r) and logical connectives (such as ~,
L
and V).
- A truth table is a table which displays the
truth values of a statement form that correspond to the different combinations of truth
values for the variables.
- Fill in the following truth tables:
|
| p |
q |
|
p L q |
| T |
T |
|
T |
| T |
F |
|
F |
| F |
T |
|
F |
| F |
F |
|
F |
|
| p |
q |
|
p V q |
| T |
T |
|
T |
| T |
F |
|
T |
| F |
T |
|
T |
| F |
F |
|
F |
|
- Two statement forms are called logically equivalent if, and only if, they have identical truth values for each possible
substitution of statements for their statement variables. The logical equivalence of
statement forms P and Q is denoted by writing P
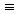 Q.
Q.
- De Morgan's Laws:
The statement ~(p L q)
is logically equivalent to the
statement ~p V ~q.
The statement ~(p V q) is logically equivalent to the
statement ~p L ~q.
- A tautology is a statement form that is always
true regardless of the truth values of the individual statements substituted for its
statement variables.
- A contradiction is a statement form that is
always false regardless of the truth values of the individual statements substituted for
its statement variables.
Exercise 1.1.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. Write the following statements in symbolic form.
a) Jane likes mathematics but does not like chemistry.
Let p be ``Jane likes mathematics'' and let q be
``Jane likes chemistry''.
Hint
Full solution
b) Jane likes neither mathematics nor chemistry but does like biology.
Let p and q be as in part a), and let r
be ``Jane likes biology''.
Hint
Full solution
c) Either Sam will come to the party and Max will not, or Sam won't come to the party
and Max will enjoy himself at the party.
Let p be ``Sam will come to the party'', let q be
``Max will come to the party'', and let r be ``Max will enjoy himself at the
party''.
Hint
Full solution
2. If p is the statement ``it is raining'' and q is the statement
``it is hot'', translate the following into English sentences.
a) p L ~q
Hint
Full solution
b) (p V q) L ~(p L q)
Hint
Full solution
3. Construct a truth table to determine the truth values for (p V q) L ~p.
There are two statement variables so the truth table will have
4 rows.
| p |
q |
|
p V q |
~p |
|
(p V q) L ~p |
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
Hint
Full solution
4. Construct a truth table to determine the truth values for (p V q)
L ~(p V r).
There are three statement variables so the truth table will have 8 rows.
| p |
q |
r |
|
p V q |
p V r |
~(p V r) |
|
(p V q) L
~(p V r) |
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
Hint
Full solution
5. Are the statement forms p L ~q
and (p V q) L ~q logically
equivalent?
There are two statement variables so the truth table will have 4 rows.
| p |
q |
|
~q |
p V q |
|
p L ~q |
(p V q) L ~q |
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
Hint
Full solution
6. Is the statement form (p L q) V (~ p
V (p L ~q)) a tautology, a contradiction, or
neither?
There are two statement variables so the truth table will have
4 rows.
| p |
q |
|
p L q |
~p |
~q |
p L ~q |
~p V (p L ~q) |
|
(p L q) V (~p
V (p L ~q)) |
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
Hint
Full solution
Section 1.2
Conditional Statements
The following solutions use information found on pages 17-25 of the textbook.
Exercise 1.2.1: Definitions
Fill in the blanks to complete the following sentences.
- If p and q are statement variables, the symbolic form of if
p then q is p
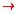 q. This
may also be read "p implies q". Here p is called the hypothesis
and q is called the conclusion.
q. This
may also be read "p implies q". Here p is called the hypothesis
and q is called the conclusion.
``If p then q'' is false when p is true
and q is false, and it is true otherwise.
- ``If p then q'' is logically equivalent to not p
or q, that is p
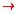 q is equivalent to ~p V q.
q is equivalent to ~p V q.
- The contrapositive of p
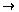 q is ~q
q is ~q 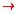 ~p.
~p.
- Given statement variables p and q, the biconditional
of p and q is p
 q. This is read "p if, and only
if, q".
q. This is read "p if, and only
if, q".
It is true when p and q have the same truth
values. It is false when p and q have
opposite truth values.
- Fill in the following truth tables:
| p |
q |
|
p 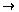 q q |
| T |
T |
|
T |
| T |
F |
|
F |
| F |
T |
|
T |
| F |
F |
|
T |
|
| p |
q |
|
p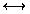 q q |
| T |
T |
|
T |
| T |
F |
|
F |
| F |
T |
|
F |
| F |
F |
|
T |
|
- The order of operations for the five logical connectives is first
~, then V and L in the order in which they appear, then
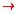 and
and  in the order in which they
appear. Note that it is always a good idea to include
brackets wherever confusion may arise.
in the order in which they
appear. Note that it is always a good idea to include
brackets wherever confusion may arise.
Exercise 1.2.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. Translate the following statements into symbolic form.
a) (i) If I am worried, I will not sleep.
(ii) I will not sleep if I am worried.
Let p be ``I will not sleep'' and let q be ``I
am worried''.
Hint
Full solution
b) If I am worried, then I will both work hard and not sleep.
Let p and q be as in part a) and let r
be ``I will work hard''.
Hint
Full solution
2. Construct a truth table to determine the truth values for p 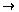 ( q
L ~p).
( q
L ~p).
There are two statement variables so the truth table will have
4 rows.
| p |
q |
|
~p |
q L ~p |
|
p 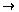 (q L ~p) (q L ~p) |
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
Hint
Full solution
3. Rewrite the following sentence in ``if--then'' form. Either you do not
study or you pass the test.
Hint
Full solution
4. Write the contrapositive of the following sentence. If you do not study, then
you will fail the test.
Hint
Full solution
5. Rewrite the statements ``I say what I mean'' and ``I mean what I say'' in if--then
form. Use a truth table to show that the two statements are not logically equivalent.
Let p be ``I say it'' and let q be ``I mean
it''.
Hint
Full solution
6. Use a truth table to show that p 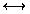 q is logically equivalent to (p
q is logically equivalent to (p 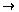 q)
L (q
q)
L (q  p).
p).
There are two statement variables so the truth table will have
4 rows.
Hint
Full solution
7. Use the result of question 6 to complete the following sentence.
p if, and only if, q is the same as
Hint
Full solution
Section 1.3
Valid and Invalid Arguments
The following solutions use information found in the Reading Section.
Exercise 1.3.1: Definitions
Fill in the blanks to complete the following sentences.
- An argument is a sequence of statements in which
the conjunction of the initial statements (called the premises) is said to imply the final
statement (called the conclusion). An argument can be
presented symbolically as (p1 L p2 L ... L pn)
 q.
q.
- An argument is valid if whenever the
premises are all true, the conclusion must also be true. That is, when (p1
L p2 L ... L pn)
 q is a tautology.
q is a tautology.
Exercise 1.3.2: Examples
You should attempt all these exercises yourself, using the information in the reading
section as an aid. Once you have attempted each question, check your answers by following
the appropriate links. If you are stuck on a question, choose the link that gives you a
hint and then try the question again.
1. Represent the following arguments in symbolic form and determine whether or not they
are valid.
a) If wages are raised, buying increases. If there is a depression, wages are not
raised. Therefore, either there is not a depression, or wages are not raised.
Let w represent ``wages are raised'', b
represent ``buying increases'', and d represent ``there is a depression''.
Hint
Solution by truth table
Solution by argument for invalidity
b) If Bill is a cheater, then Bill sits in the back row. Bill sits in the back row.
Therefore Bill is a cheater.
Let c represent ``Bill is a cheater'' and s
represent ``Bill sits in the back row''.
Hint
Solution by truth table
Solution by argument for invalidity
c) If the cat fiddled or the cow jumped over the moon, then the little dog laughed. If the
little dog laughed, then the dish ran away with the spoon. But the dish did not run away
with the spoon. Therefore the cat did not fiddle.
Let c represent ``the cat fiddled'', j
represent ``the cow jumped over the moon'', d represent ``the little dog
laughed'', and r represent ``the dish ran away with the spoon''.
Hint
Solution by truth table
Solution by argument for invalidity
Section 1.4
Application: Digital Logic Circuits
The following solutions use information found on pages 41-53 of the textbook.
Exercise 1.4.1: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. Indicate the output of the circuit below when the input signals are P=1, Q=0 and
R=0.
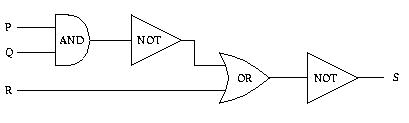
Output: S =
Hint
Full solution
2. Construct the input/output table for the following circuit:
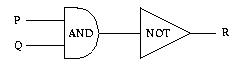
There are two inputs so our table will have 4 rows.
Hint
Full solution
3. Find a Boolean Expression for the circuit below and determine which
combination of inputs this circuit recognizes.
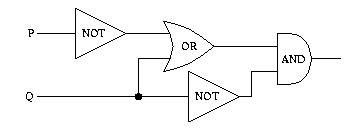
Hint
Full solution
Back to workbook solution page