1a) Let w represent "wages are raised", let b represent "buying increases", and let d represent "there is a depression."
The first premise (p1) is "If wages are raised, then
buying increases." This can be written symbolically as w
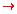b.
The second premise (p2) is "If there is a depression, then wages are not
raised." This can be written symbolically as d 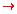~w.
The conclusion (q) is "Therefore, either there is not a depression, or wages are not
raised." This can be written symbolically as ~d
V ~w.
Remember that an argument is written as a conjunction of the premises
implies the conclusion. So this argument can be represented as
[(w 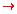b) L (d 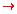~w)]
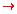(~d V ~w).
Now construct a truth table.
| w | b | d | w  b |
d ~w |
~d V ~w | ||
| T | T | T | T | F | F | ||
| T | T | F | T | T | T | ||
| T | F | T | F | F | F | ||
| T | F | F | F | T | T | ||
| F | T | T | T | T | T | ||
| F | T | F | T | T | T | ||
| F | F | T | T | T | T | ||
| F | F | F | T | T | T |
The critical rows of the truth table are the rows in which all the premises are true. Identify these rows. An argument is valid if the conclusion is true in all the critical rows.