Chapter Two

The Logic of Quantified Statements

Section 2.1

Predicates and Quantified Statements I

The following solutions use information found on pages 75-87 of the textbook.

Exercise 2.1.1:  Definitions

Fill in the blanks to complete the following sentences.

1. A predicate is a sentence that contains a finite number of variables and becomes a statement when specific values are substituted for the variables.
2. The domain of a predicate variable is the set of all values that may be substituted in place of the variable.
3. The symbol R represents the set of real numbers.
   Examples of elements of R include 4, 7.8, p, ¼.
4. The symbol Z represents the set of integers.
   Examples of elements of Z include -3, 5, 0, -100, 3519.
5. The symbol Q represents the set of rational numbers.
   Examples of elements of Q include ½, 4.56, 0, ¾.
6. The symbol " denotes for all. Note that the collection of mathematical symbols " x 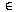D, is read "for all x belonging to the set D".
   The statement "" x 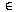D, S(x)"  is true, if and only if, the statement S(x) is true for every element x of the set D,
   and is false if, and only if, S(x) is false for at least one element x of the set D.
7. The symbol $ denotes there exists. Note that the collection of mathematical symbols $ x 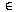D, is read "there exists an element x belonging to the set D".
   The statement "$ x 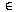D such that S(x)'' is true, if and only if, the statement S(x) is true for at least one element x of the set D,
   and is false if, and only if, S(x) is false for every element x of the set D.
8. The negation of "" x 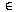D, S(x)'' is $ x 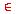D such that ~S(x).
9. The negation of "$ x 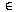D such that S(x)'' is  " x 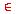D, ~S(x).
10. The negation of "" x 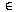D,  if  P(x)  then S(x)'' is $ x 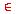D such that P(x) L ~S(x). Recall that  ~(p 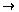q)  is  ~(~p V q)  which is   p L ~q.
    
    

Exercise 2.1.2:  Examples

You should attempt all these exercises yourself, using the textbook as an aid. Once you have attempted each question, check your answers by following the appropriate links. If you are stuck on a question, choose the link that gives you a hint and then try the question again.

1. Let P(x) be the predicate "10 is a factor of x'', and let S(x) be the predicate "5 is a factor of x''. Suppose the domain of x is {1,2,..., 99}.
Determine the truth sets for P(x) and S(x) and indicate the relationship between P(x) and S(x) using some of the symbols ", $, 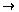and .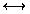

Hint
Full solution

2. Determine whether the following statements are true or false. Here in parts a) and b) R represents the real numbers, and in parts c) and d) let A be the set
{1,2,3}.

a) " x 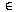R, x² = 2.

Hint
Full solution

b) $ x 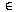R such that x² = 2.

Hint
Full solution

c) " x 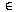A, x² < 10.

Hint
Full solution

d) $ x 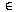A such that x > 4.

Hint
Full solution

3. Translate the following statements into informal English sentences.

a) " squares s, s is a rectangle. 

Hint
Full solution

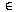b) $ x R such that x 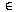Q (the set of rational numbers).

Hint
Full solution

4. Negate the following statements and state which of the statements (the original or the negation) is true.

a) " x 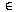Z, x is even.

Hint
Full solution

b) $ y 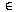R such that y² < 0.

Hint
Full solution

5. Write the statement "if an integer has a factor of 4, then it also has a factor of 2" in symbolic form. Then write the negation of this statement.

Let F(x) be the predicate "4 is a factor of x" and let T(x) be the predicate "2 is a factor of x".

Hint
Full solution

Section 2.2

Predicates and Quantified Statements II

The following solutions use information found on pages 89-92 of the textbook.

Exercise 2.2.1:   Definitions

Fill in the blanks to complete the following sentences.

1. The negation of      " x, $ y such that P(x,y)     is      $ x such that " y, ~P(x,y).
2. The negation of      $ x such that " y, P(x,y)      is    " x, $ y such that ~P(x,y).
   
   

Exercise 2.2.2:  Examples

You should attempt all these exercises yourself, using the textbook as an aid. Once you have attempted each question, check your answers by following the appropriate links. If you are stuck on a question, choose the link that gives you a hint and then try the question again.

1. Translate the following statements into English sentences.

a) " x 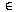Z, $ y 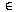Z such that x² = y².

Hint
Full solution

b) $ a person p such that " languages l, p speaks l.

Hint
Full solution

2. Translate the following statements into symbolic form.

a) There is a child with no siblings.

Hint
Full solution

b) Every integer is divisible by at least one prime number.

Hint
Full solution

3. Negate the following statement: $ x 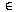R such that " y 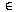R, xy = 0. Then determine which statement is true, the original or the negation.

Hint
Full solution

Back to workbook solutions page