Chapter Seven
Functions
Section 7.1
The Definition of a Function
The following solutions make use of information found on pages 344 - 354 of the
textbook.
Exercise 7.1.1: Definitions
Fill in the blanks to complete the following sentences.
- A function f from a set X to a set Y is
a relation
from the set X to the set Y with the property that each element of X is
related to a unique element of Y.
- The notation f: X
 Y
is read f is a function from X to Y.
Y
is read f is a function from X to Y.
- The definition of a function f: X
 Y states that given
an element x in X, there is a unique element y
in Y
that is related to x. We write y = f(x), read
y equals f of x.
Y states that given
an element x in X, there is a unique element y
in Y
that is related to x. We write y = f(x), read
y equals f of x.
We say x is mapped under f to y or we say f
sends x to y and write x
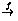 y
or x
y
or x  f(x).
f(x).
We can think of x as the input and y as the
related output.
Equivalently, the value of f at x is denoted
f(x) and
the image of x under f is denoted
f(x).
- The domain of the function f: X
 Y
is the set
X and the co-domain
of the function f is the set
Y.
Y
is the set
X and the co-domain
of the function f is the set
Y.
- The range of a function f: X
 Y is the set of
y
Y is the set of
y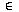 Y such that y = f(x) for some
x
Y such that y = f(x) for some
x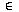 X.
Symbolically the range of f is:
X.
Symbolically the range of f is:
{ y 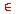 Y |
y = f(x), for some x in X}.
Y |
y = f(x), for some x in X}.
- Given a function f: X
 Y and an element
y
Y and an element
y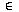 Y, the inverse image of y is the
set of all elements
x
Y, the inverse image of y is the
set of all elements
x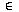 X such that f(x) = y. Symbolically the
inverse image of y is:
X such that f(x) = y. Symbolically the
inverse image of y is:
{ x 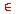 X |
f(x) = y}.
X |
f(x) = y}.
- An arrow diagram for a function has the following two properties:
1. Every element of X has an arrow coming out of it;
2. No element of X has two arrows coming out of it that point to two
different elements of Y.
- Suppose f and g are functions from a set X to a
set Y. Then
f equals g, written f = g, if, and only if, f(x) = g(x) for
all x
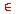 X.
X.
- The special function iX from the set X to X is
called the identity funtion on X and for all x
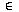 X, iX(x)
= x.
X, iX(x)
= x.
- Previously we said that a sequence was a list of elements.
More formally, a sequence is a function whose
domain is the set of integers that are greater than or equal
to a particular integer. (See page 349 of your textbook for
an example of this.)
Exercise 7.1.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
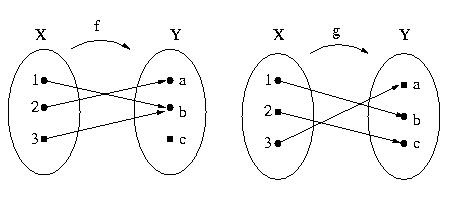
1. Let f be the function defined by the arrow diagram below:
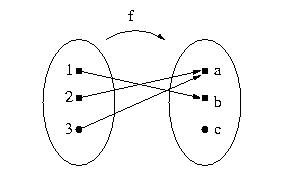
a) Write down the domain and co-domain of f.
b) Find f(1), f(2) and f(3).
c) What is the range of f?
d) Find the inverse images of a, b and c.
Full solution
2. Which of the following define functions? Explain your answer.
| a) |
b) |
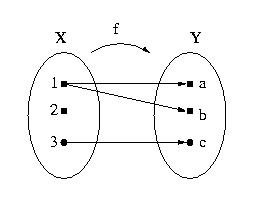
|
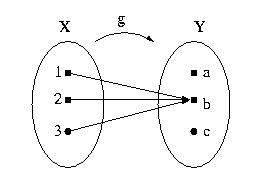
|
Hint
Full solution
3.a) Define functions f : R R and g : R
R and g : R R, where
f(x) = x for all x
R, where
f(x) = x for all x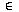 R
and g(x) =
R
and g(x) = 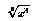 for all x
for all x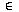 R. Is f = g? Explain your answer.
R. Is f = g? Explain your answer.
b) Define functions f : R R and g : R
R and g : R R, where
f(x) = x for all x
R, where
f(x) = x for all x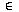 R
and g(x) =
R
and g(x) = 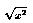 for all x
for all x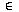 R. Is f = g? Explain
your answer.
R. Is f = g? Explain
your answer.
Hint
Full solution
4. Write the sequence -4, 9, -16, 25, ... as a function.
Hint
Full solution
5. Read Example 7.1.11 on pages 351 - 352 of the textbook. Then use the Hamming
distance function to calculate H(1100101, 0010111).
Hint
Full solution
6. A binary operation on a set X is a special kind of function from X
× X to X. One example of a binary operation is addition on the set Z.
Let f: Z × Z  Z be the function of addition
on the integers.
Z be the function of addition
on the integers.
a) Evaluate f((3,2)).
b) Find an element of Z × Z with an image of -1.
Hint
Full solution
7. Suppose you are told that a function f: Q  Z is to
be defined by the formula f( m/n) = n for all integers m and n where
n
Z is to
be defined by the formula f( m/n) = n for all integers m and n where
n 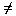 0. Is f well-defined?
Justify your answer.
0. Is f well-defined?
Justify your answer.
Hint
Full solution
Section 7.2
Application: Finite-State Automata
The following solutions make use of information found on pages 357 - 364 of the
textbook.
Exercise 7.2.1: Definitions
Fill in the blanks to complete the following sentences.
- A finite-state automaton A consists of five objects:
1. a set I of input symbols, called the input
alphabet;
2. a set S of states in which the automaton can be;
3. a designated state s0, called the initial state;
4. a designated set of states called the set of accepting states;
5. a next-state function N: S × I  S that associates a
"next-state" to each ordered pair consisting of a "current state" and
a "current input". For each state s in S and input symbol m in I, N(s,m)
is the state to which A goes if m is input to A when A is in state s.
S that associates a
"next-state" to each ordered pair consisting of a "current state" and
a "current input". For each state s in S and input symbol m in I, N(s,m)
is the state to which A goes if m is input to A when A is in state s.
- A (state-)transition diagram is often used to describe the operation of
a finite-state automaton. It shows the transitions the
machine makes from one state to another in response to various inputs.
- A next-state table for an automaton shows the
values of the next-state function N for all possible states s and input symbols i.
- Let A be a finite-state automaton and let I be the input
alphabet. Let I* denote
the set of strings over the alphabet I, and let w
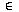 I*; that is, let w be a string consisting of symbols chosen
from the alphabet I.
Then w is
accepted by A if, and only if, A goes to an accepting state
when the symbols of w are input to A in sequence starting when A is in
its initial state.
I*; that is, let w be a string consisting of symbols chosen
from the alphabet I.
Then w is
accepted by A if, and only if, A goes to an accepting state
when the symbols of w are input to A in sequence starting when A is in
its initial state.
The language accepted by A, denoted L(A), is the
set of all strings that are accepted by A.
- Let A be a finite-state automaton with set of states S and input
alphabet I. Let I* denote the set of strings over the
alphabet I and
N: S × I
 S denote the next-state function. Then
the eventual-state function
N*: S × I*
S denote the next-state function. Then
the eventual-state function
N*: S × I*
 S is defined as follows:
S is defined as follows:
For any state s and for any input string w, N*(s,w) = the state to which A goes if the symbols of w are input to A in sequence
starting when A is in state s.
Exercise 7.2.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. A vending machine dispenses jaw-breakers that cost 20¢ each. The machine accepts
5¢, 10¢ and 20¢ pieces only and does not give change. As soon as the amount
deposited equals or exceeds 20¢, the machine releases a jaw-breaker. The next coin
deposited starts (from zero) the process over again.
Draw a transition diagram for this finite-state automaton.
Hint
Full solution
2. Consider the finite-state automaton A defined by the transition diagram below:

a) What are the states of A?
b) What are the input symbols of A?
c) What is the initial state of A?
d) What are the accepting states of A?
e) Find N(t1, 1) and N(t3, 0).
f) Create the annotated next-state table for A.
Hint
Full solution
3. Consider the finite-state automaton A defined by the following next-state table:
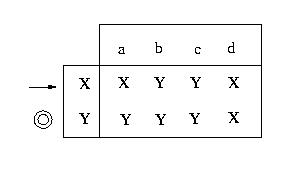
a) What are the states of A?
b) What are the input symbols of A?
c) What is the initial state of A?
d) What are the accepting states of A?
e) Find N(X, b) and N(Y, a).
f) Draw the transition diagram for A.
Hint
Full solution
4. Refer back to Question 2.
a) To which states would the automaton go for each of the following strings of input
symbols?
i) 01 ii) 0010 iii)
11000 iv) 111
b) Which of the strings from part a) send the automaton to an accepting state?
c) What is the language accepted by this automaton?
Hint
Full solution
5. Refer again to Question 2. Find N*(t2, 00100).
Hint
Full solution
Section 7.3
One-to-One and Onto, Inverse Functions
The following solutions make use of information found on pages 369 - 384 of the
textbook.
Exercise 7.3.1: Definitions
Fill in the blanks to complete the following sentences.
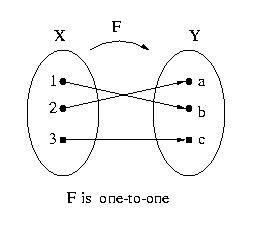
- Let F be a function from a set X to a set Y. F is
one-to-one (or
injective) if, and only if, for all elements x1 and
x2 in X, if F(x1) =
F(x2), then x1 = x2.
The contrapositive statement is:
"
x1, x2 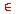 X,
if x1
X,
if x1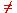 x2,
then F(x1)
x2,
then F(x1)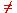 F(x2).
F(x2).
- A function F: X
 Y
is not one-to-one if, and only if,
$
x1, x2 in X such that
F(x1) = F(x2) and x1
Y
is not one-to-one if, and only if,
$
x1, x2 in X such that
F(x1) = F(x2) and x1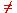 x2.
x2.
- To show that a function f: X
 Y is one-to-one, you usually suppose that x1 and x2 are elements of X such that f(x1)
= f(x2) and show that x1 = x2.
Y is one-to-one, you usually suppose that x1 and x2 are elements of X such that f(x1)
= f(x2) and show that x1 = x2.
- To show that a function f: X
 Y is not one-to-one, you usually find elements
x1 and x2 in X so that f(x1) = f(x2) but x1
Y is not one-to-one, you usually find elements
x1 and x2 in X so that f(x1) = f(x2) but x1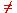 x2.
x2.
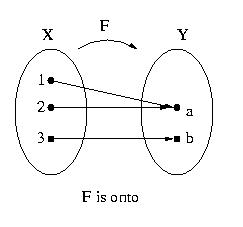
- Let F be a function from a set X to a set Y. F is onto
(or surjective)
if, and only if,
" y in Y, $
x in X such that y = F(x).
That is, for all y in Y there exists an x in X such that y is the
image of x under F
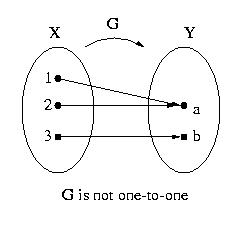
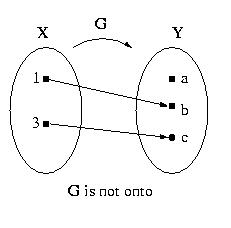
- A function F: X
 Y is not
onto if, and only if,
$ y in Y
such that "
x in X, F(x)
Y is not
onto if, and only if,
$ y in Y
such that "
x in X, F(x)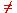 y.
y.
- To show that a function f: X
 Y is onto, you
usually suppose that y
is an arbitrary element of Y and show that
there is an element x in X
such that f(x) = y.
Y is onto, you
usually suppose that y
is an arbitrary element of Y and show that
there is an element x in X
such that f(x) = y.
- To show that a function f: X
 Y is not onto, you
usually find an
element y in Y such that y
Y is not onto, you
usually find an
element y in Y such that y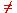 f(x) for any x in X.
f(x) for any x in X.
- A one-to-one correspondence (or bijection) from a set X to a set Y is a function F: X
 Y that is both one-to-one and onto.
Y that is both one-to-one and onto.
- Suppose that the function F: X
 Y is both
one-to-one and onto; that is, F is a
one-to-one correspondence from X to Y.
Y is both
one-to-one and onto; that is, F is a
one-to-one correspondence from X to Y.
Then there exists a
function F-1: Y X
such that for any element y in Y,
X
such that for any element y in Y,
F-1(y) = the unique
element x in X such that F(x) = y.
The function F-1 is called the inverse
function for F.
- Given a function F: X
 Y, for which
there exists an inverse function
F-1: Y
Y, for which
there exists an inverse function
F-1: Y X, then
F-1(y) = x
X, then
F-1(y) = x
 y = F(x).
y = F(x).
Exercise 7.3.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. Which of the following functions are one-to-one? Which of them are onto?
Hint
Full solution
2. Define the functions f: R R and g: R
R and g: R R
by f(x) = | x | + 1 and g(x) = 2x3-1, for all x in R.
Are these functions one-to-one? In each case either prove that the function is one-to-one
or give a counterexample to show that it is not one-to-one.
R
by f(x) = | x | + 1 and g(x) = 2x3-1, for all x in R.
Are these functions one-to-one? In each case either prove that the function is one-to-one
or give a counterexample to show that it is not one-to-one.
Hint
Full solution
3. Searching through long lists is a slow process. One way to speed up the search is to
divide the long list into a number of smaller lists. If we have some method of quickly
identifying in which of the smaller lists a particular item will appear, then we need only
search through the smaller list to find the item.
Suppose we wish to maintain the customer records for a large company and begin by
assigning each customer a unique 7-digit account number. This 7-digit number will be used
as input to a function H which will determine the sublist to be searched to find the
account details. The company has 30,000 customers and we are going to partition the
list of accounts into 100 sublists of approximately 300 items each. We define a hash
function which maps each 7-digit account number, say n, to an element x in the set {0, 1,
2, 3, ..., 99}, such that H(n) = x, where n mod 100 = x.
a) Calculate to which sublists each of the following account numbers would be
allocated.
i) 2473871 ii) 3569842 iii)
9085000 iv) 8574642
b) Is the function H one-to-one? Explain.
Hint
Full solution
4. Define the functions F: R R+ È
{0} and G: Z
R+ È
{0} and G: Z Z by F(x) = x2 for all x
in R and G(x) = x2 for all x in Z. Are
these functions onto? In each case either prove that the function is onto or give a
counterexample to show that it is not onto.
Z by F(x) = x2 for all x
in R and G(x) = x2 for all x in Z. Are
these functions onto? In each case either prove that the function is onto or give a
counterexample to show that it is not onto.
Hint
Full solution
5. Define the function F: R R by F(x) = 2x + 4 for
all x in R. Show that F is onto.
R by F(x) = 2x + 4 for
all x in R. Show that F is onto.
Hint
Full solution
6. Is the function f: X Y a one-to-one correspondence, where X = {0, 1, 2, 3} and Y
= {0, 1, 4, 9} and f(x) = x2 for all x in X? Justify your answer.
Y a one-to-one correspondence, where X = {0, 1, 2, 3} and Y
= {0, 1, 4, 9} and f(x) = x2 for all x in X? Justify your answer.
Hint
Full solution
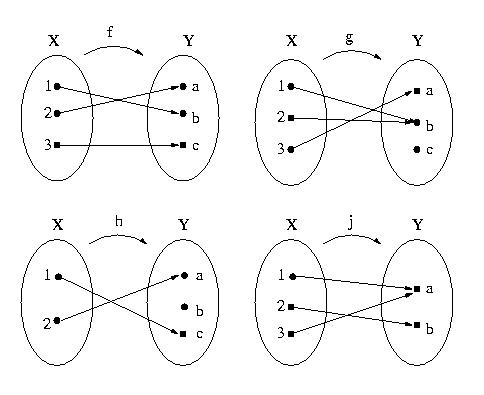
7. Given the functions f and g illustrated in the following arrow diagrams, find (if
they exist) f-1 and g-1. If they do exist, draw their arrow diagram.
Hint
Full solution
8. Find (if it exists) the inverse of the function g: R R
where g(x) = 2x + 5 for all x in R.
R
where g(x) = 2x + 5 for all x in R.
Hint
Full solution
Section 7.4
Application: The Pigeonhole Principle
The following solutions make use of information found on pages 387 - 399 of the
textbook.
Exercise 7.4.1: Definitions
Fill in the blanks to complete the following sentences.
- Recall that for a set A, n(A) denotes the number of elements in set
A.
- Pigeonhole Principle:
A function, f, from the set X to the set Y, where n(X) > n(Y),
cannot be one-to-one. There must be at least two
elements in the domain that have
the same image in the co-domain.
- Generalized Pigeonhole Principle:
Let k be a positive integer and f a function from a finite set X to a
finite set Y.
If n(X) > k · n(Y), then there is some y
in Y such that y is the
image of at least k + 1 distinct elements of X.
- A set is called finite if, and only if, it is
the
empty set or there is a one-to-one correspondence from {1, 2, 3, ..., n}
to the set, where n is
a positive integer.
In the first case, the number of elements in the set is
zero, and in the
second case it is n.
A set that is not finite is called infinite.
- Theorem Pigeonhole Principle
For any function f from a finite set X to a finite set Y, if
n(X)
> n(Y), then f is not one-to-one.
- Theorem:
Let X and Y be finite sets with the same number of elements and suppose f is a function
from X to Y. Then f is one-to-one if, and only if,
f is onto.
Exercise 7.4.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. How many students must be in a class to guarantee that at least two students receive
the same mark on the final exam which is graded on a scale of 0 to 100, (with no half
marks allowed)?
Hint
Full solution
2. There are 680 people on a list. Must there be at least two people on the list with
the same first and last initials? Justify your answer.
Hint
Full solution
3. The Prime Minister is packing to go to an important meeting in Asia, but there is a
sudden black-out and so he is fumbling around in the dark. He is reaching into his
wardrobe to find a tie to wear at the meeting. He has 12 ties, five ties that he likes and
seven that he doesn't like. How many ties must he pull out of his wardrobe to be
guaranteed of having at least one tie that he likes?
Full solution
4. Show that in a group of 25 people, at least three must have the same astrological
star sign.
Hint
Full solution
5. Assume that in a group of six people, each pair of individuals are either friends or
enemies. Show that there are either three mutual friends or three mutual enemies in the
group.
Hint
Full solution
Section 7.5
Composition of Functions
The following solutions make use of information found on pages 401 - 410 of the
textbook.
Exercise 7.5.1: Definitions
Fill in the blanks to complete the following sentences.
- Let f: X
 Y and g: Y
Y and g: Y Z be functions with the
property that the range of f is a subset of the domain of g.
Define a new function g
o f: X
Z be functions with the
property that the range of f is a subset of the domain of g.
Define a new function g
o f: X Z as follows:
Z as follows:
(g o
f )(x) = g( f (x) ) for all x in X.
The function g o f is called the
composition of f and g.
We read g o f as "g
circle f " and
g( f (x) ) as "g of f of
x".
Label the following diagram to illustrate the function g o
f.
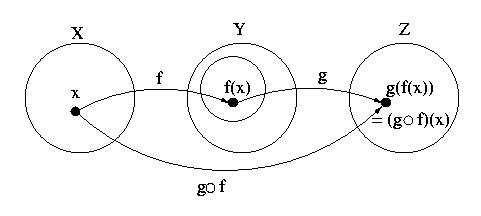
- Theorem:
Let f be a one-to-one correspondence from a set X to a set Y. Then
the inverse function exists and can be denoted by
f-1: Y X. It follows that
X. It follows that
f -1 o f = iX
and f o f
-1 = iY.
Exercise 7.5.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. Let f: R R be defined by f(x) = x3
for all x
R be defined by f(x) = x3
for all x R
and let g: R
R
and let g: R R be defined by g(x) = 2x - x2
for all x
R be defined by g(x) = 2x - x2
for all x R.
R.
a) Find (f o g)(x) and (g o
f)(x).
b) Is g o f = f o g?
Hint
Full solution
2. Let X = {a, b, c}, Y' = {1, 2, 3}, Y = {1, 2, 3, 4} and Z = {w, x, y, z}. Define
the functions f: X Y'
and g: Y
Y'
and g: Y Z by the
diagram below.
Z by the
diagram below.

a) Draw the arrow diagram for g o f.
b) What is the range of g o f?
Hint
Full solution
3. Suppose that f: Z Z is a function where f (x) = x + 1 for all
x
Z is a function where f (x) = x + 1 for all
x Z. Let iZ be the identity function.
Z. Let iZ be the identity function.
a) Find ( f o iZ )(x) and
( iZ o f
)(x).
b) If g: X X
is any function, what can you say about the functions g o iX
and iX o g?
X
is any function, what can you say about the functions g o iX
and iX o g?
Hint
Full solution
4. Let f and g be functions defined by the arrow diagrams below.
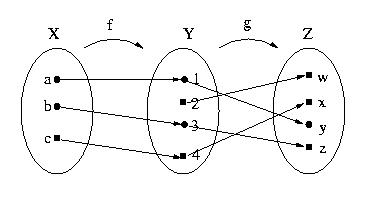
a) Draw the arrow diagram representing g o f.
b) f and g are both one-to-one. Is g o f one-to-one?
Hint
Full solution
5. Let F and G be functions defined by the arrow diagrams below.
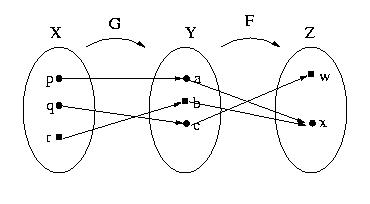
a) Draw the arrow diagram representing F o G.
b) F and G are both onto. Is F o G onto?
Hint
Full solution
Section 7.6
The Cardinality of a Set (Extension Material)
The following solutions make use of information found on pages 411 - 416 of the
textbook.
Exercise 7.6.1: Definitions
Fill in the blanks to complete the following sentences.
- Recall that a finite set is either
the empty set
or a set that has a one-to-one correspondence
with a set of the
form {1, 2, 3, ..., n} for some positive integer n.
An infinite set is a nonempty
set that cannot be
put into one-to-one correspondence with the set {1, 2, 3, ..., n} for
any positive integer
n.
- Let A and B be any sets. Sets A and B are said to have
the same cardinality if, and
only if, there is a one-to-one correspondence
from A to B.
In other words, A has the same cardinality as B if,
and only if,
there is a function from A to B that is one-to-one and onto.
- A set is said to be countably infinite if, and only if,
it has the same cardinality as the set of positive
integers Z+.
A set is said to be countable if, and only if,
it is
finite or countably infinite.
A set that is not countable is said to be uncountable.
- Recall that a function from one finite set to another set of the
same size is one-to-one if, and only if, it is onto.
This result does not hold for
infinite sets.
Exercise 7.6.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. Show that the set of all odd integers is countable.
Hint
Full solution
2. Show that there is no one-to-one correspondence between a set X and its power set
P(X).
Hint
Full solution
3. Verify that the set P(Z+) is uncountable.
Hint
Full solution
Back to workbook solution page